LeetCode 994 LintCode 3726 Rotting Oranges

Table of contents

Description

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

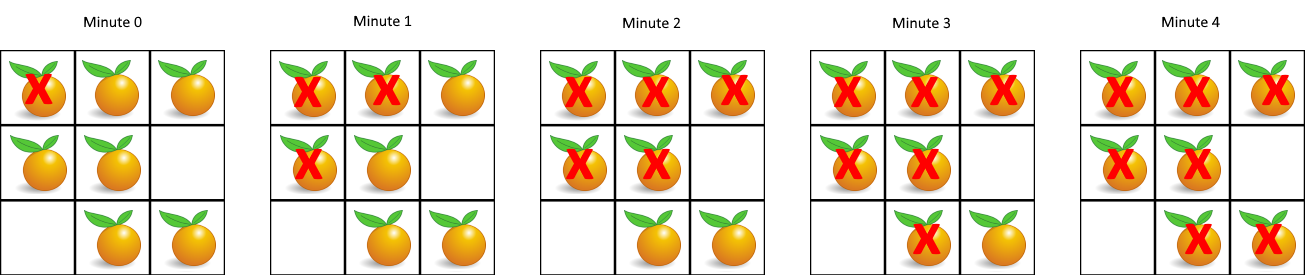
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4
Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] is 0, 1, or 2.

Idea

We could use breadth-first-search (BFS) to explore the graph starting from the rotten oranges.

1. We add the rotten orange locations to a queue and maintain the count of fresh oranges.
2. If fresh count becomes zero or the queue is empty, we can stop exploring.
3. Every iteration, we start from the rotten oranges and explore the four directions. We change the fresh orange neighbors to rotten and add the locations to the queue.
4. If the fresh count can reach to zero, we return the number of steps during the BFS. Otherwise, return -1.

Complexity: Time $O(nm)$, Space $O(nm)$.

Python

class Solution:
    """6 ms, 17.32 mb"""

    def orangesRotting(self, grid: list[list[int]]) -> int:
        (m, n), fresh, q, res = map(len, (grid, grid[0])), 0, deque(), 0
        for r in range(m):
            for c in range(n):
                if grid[r][c] == 2:
                    q.append((r, c))
                elif grid[r][c] == 1:
                    fresh += 1
        while q and fresh > 0:
            res += 1
            for _ in range(len(q)):
                x, y = q.popleft()
                for dx, dy in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
                    nx, ny = x + dx, y + dy
                    if nx < 0 or nx == m or ny < 0 or ny == n: continue
                    if grid[nx][ny] == 0 or grid[nx][ny] == 2: continue
                    fresh -= 1
                    grid[nx][ny] = 2  # serve as visited
                    q.append((nx, ny))
        return res if fresh == 0 else -1

Rust

A couple caveats.

1. If using usize for row and column indices, we can use usize::MAX to replace -1 in the four directions.
2. No need to check boundary less than 0 since usize was used.

use std::collections::VecDeque;

/// leet 994, 0 ms, 2.25 mb
impl Solution {
    pub fn oranges_rotting(mut grid: Vec<Vec<i32>>) -> i32 {
        let (m, n, mut res, mut fresh, mut q) = (grid.len(), grid[0].len(), 0, 0, VecDeque::new());
        for i in 0..m {
            for j in 0..n {
                match grid[i][j] {
                    2 => q.push_back((i, j)),
                    1 => fresh += 1,
                    _ => {}
                }
            }
        }
        while !q.is_empty() && fresh > 0 {
            for _ in 0..q.len() {
                let (x, y) = q.pop_front().expect("not empty");
                for (dx, dy) in vec![(0, usize::MAX), (usize::MAX, 0), (0, 1), (1, 0)] {
                    let (nx, ny) = (x + dx, y + dy);
                    if nx > m - 1 || ny > n - 1 || grid[nx][ny] == 2 || grid[nx][ny] == 0 { continue; }
                    fresh -= 1;
                    grid[nx][ny] = 2;
                    q.push_back((nx, ny));
                }
            }
            res += 1;
        }
        if fresh == 0 { res } else { -1 }
    }
}