Table of contents
Open Table of contents
Description
There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [ai, bi] represents a connection between servers ai and bi. Any server can reach other servers directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some servers unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
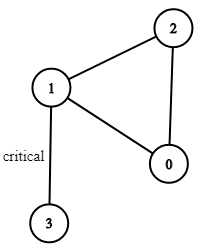
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.
Example 2:
Input: n = 2, connections = [[0,1]]
Output: [[0,1]]
Constraints:
2 <= n <= 10^5
n - 1 <= connections.length <= 10^5, e
0 <= a_i, b_i <= n - 1
a_i != b_i
There are no repeated connections.
Solution
Idea
We can use Tarjan’s algorithm to traverse the graph and try to find the topological order. If we encounter a cycle, the edges in the cycle are not critical. We set the rank for the vertexes in the cycle to the minimum rank.
Let’s use example 1 above and go through the iterations of the dfs.
| dfs(parent,vertex,rank) | ranks | res | explanation |
|---|---|---|---|
dfs(0,0,1) | [0,0,0,0] | [] | init |
dfs(0,0,1) | [1,0,0,0] | [] | ranks[0]=1 |
dfs(0,1,2) | [1,2,0,0] | [] | dfs 1 from 0, ranks[1]=2 |
dfs(1,2,3) | [1,2,0,3] | [] | dfs 2 from 1, ranks[2]=3 |
dfs(2,1,3) | no change | [] | 1 is parent, no need to dfs |
dfs(2,0,4) | no change | [] | ranks[0]!=0, no need to dfs |
dfs(2,1,3) | [1,2,1,0] | [] | ranks[2] reduce to 1 |
dfs(0,1,2) | [1,1,1,0] | [] | ranks[1] reduce to 1 |
dfs(1,3,3) | [1,1,1,3] | [[1,3]] | ranks[3]=3, skip dfs 1 (parent) |
dfs(0,0,1) | no change | no change | look at vertex 2 |
dfs(0,2,2) | no change | no change | ranks[2]!=0, no need to dfs |
dfs(0,0,1) | no change | no change | nothing to do |
| all done |
Complexity: Time O(n+e), Space O(n+e).
C++
class Solution {
vector<int> ranks;
vector<vector<int>> res;
vector<vector<int>> adj;
public:
vector<vector<int>> criticalConnections(int n, vector<vector<int>> &connections) {
adj.resize(n);
ranks.resize(n);
for (auto &e: connections)
adj[e[0]].emplace_back(e[1]), adj[e[1]].emplace_back(e[0]);
for (int v = 0; v < n; v++) dfs(0, v, 1);
return res;
}
void dfs(int p, int v, int rank) {
if (ranks[v] != 0) return;
ranks[v] = rank;
for (int w: adj[v]) {
if (w == p) continue;
dfs(v, w, rank + 1);
ranks[v] = min(ranks[v], ranks[w]);
if (rank < ranks[w]) res.emplace_back(initializer_list<int>{v, w});
}
}
};