LeetCode 2257 Count Unguarded Cells in the Grid

Table of contents

Description

You are given two integers m and n representing a 0-indexed m x n grid. You are also given two 2D integer arrays guards and walls where guards[i] = [rowi, coli] and walls[j] = [rowj, colj] represent the positions of the ith guard and jth wall respectively.

A guard can see every cell in the four cardinal directions (north, east, south, or west) starting from their position unless obstructed by a wall or another guard. A cell is guarded if there is at least one guard that can see it.

Return the number of unoccupied cells that are not guarded.

Example 1:

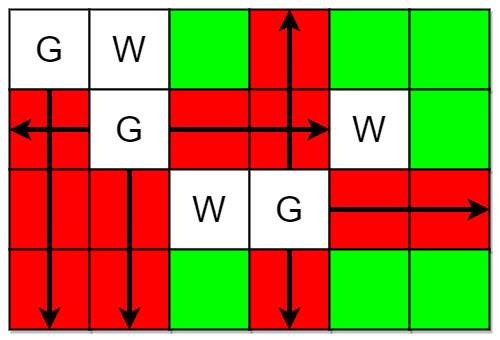
Input: m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]
Output: 7
Explanation: The guarded and unguarded cells are shown in red and green respectively in the above diagram.
There are a total of 7 unguarded cells, so we return 7.

Example 2:

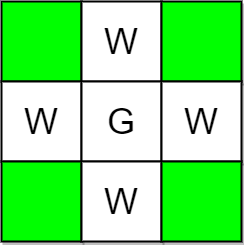
Input: m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]]
Output: 4
Explanation: The unguarded cells are shown in green in the above diagram.
There are a total of 4 unguarded cells, so we return 4.

Constraints:

• 1 <= m, n <= 10^5
• 2 <= m * n <= 10^5
• 1 <= guards.length, walls.length <= 5 * 10^4
• 2 <= guards.length + walls.length <= m * n
• guards[i].length == walls[j].length == 2
• 0 <= row_i, row_j < m
• 0 <= col_i, col_j < n
• All the positions in guards and walls are unique.

Hint 1

Create a 2D array to represent the grid. Can you mark the tiles that can be seen by a guard?

Hint 2

Iterate over the guards, and for each of the four directions, advance the current tile and mark the tile. When should you stop advancing?

Solution

let g = number of guards

Idea1

Intuition: We could start from the guard positions and scan the four directions to mark the reachable cells as guarded. To do that, we need to mark the positions of the guards and walls, so we can stop scanning when the sight is blocked. Finally, we iterate through all the cells and count the unguarded ones.

1. We could instantiate a matrix to record the state of the cells: unguarded, guard position, wall, or guarded.
2. We mark the positions for the guards and the walls. O(mn) time.
3. For each guard, we scan the four directions. Stop when the sight is blocked. O(g(m+n)) time.
4. Final count. O(mn) time.

Complexity: Time O(mn+g(m+n)), Space O(mn).

Java

class Solution {
    static final int UNGUARDED = 0, GUARDED = 1, GUARD = 2, WALL = 3;
    static int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    int[][] grid; // probabl cannot trust leetcode memory profiler, char 78.7Mb, int 66.8Mb.

    void markGuarded(int r, int c) {
        int m = grid.length, n = grid[0].length;
        for (int[] d : dirs) {
            int nx = r + d[0], ny = c + d[1];
            while (!(nx < 0 || ny < 0 || nx >= m || ny >= n || grid[nx][ny] == GUARD || grid[nx][ny] == WALL)) {
                grid[nx][ny] = GUARDED;
                nx += d[0];
                ny += d[1];
            }
        }
    }

    public int countUnguarded(int m, int n, int[][] guards, int[][] walls) {
        grid = new int[m][n];
        for (int[] guard : guards) grid[guard[0]][guard[1]] = GUARD;
        for (int[] wall : walls) grid[wall[0]][wall[1]] = WALL;
        for (int[] g : guards) markGuarded(g[0], g[1]);
        int res = 0;
        for (int[] row : grid)
            for (int cell : row) if (cell == UNGUARDED) res++;
        return res;
    }
}

Idea2

We can optimize the above approach.

1. We can use char[][] in Java to reduce some space. This is a 50 % saving.
2. Instead of counting unguarded cells at the end, we can decrement the guarded cells from the total.

Complexity: Time O(mn+g(m+n)), Space O(mn).

Java

class Solution {
    public int countUnguarded(int m, int n, int[][] guards, int[][] walls) {
        int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
        char[][] grid = new char[m][n];
        int res = m * n - guards.length - walls.length;
        for (int[] w : walls) grid[w[0]][w[1]] = 'W';
        for (int[] g : guards) grid[g[0]][g[1]] = 'G';
        for (int[] g : guards) {
            for (int[] d : dirs) {
                int nx = g[0] + d[0], ny = g[1] + d[1];
                while (!(nx < 0 || ny < 0 || nx >= m || ny >= n || grid[nx][ny] == 'G' || grid[nx][ny] == 'W')) {
                    if (grid[nx][ny] != 'P') res--;
                    grid[nx][ny] = 'P';
                    nx += d[0];
                    ny += d[1];
                }
            }
        }
        return res;
    }
}