LeetCode 2017 Grid Game

Table of contents

Description

Link to Question: LeetCode 2017

You are given a 0-indexed 2D array grid of size 2 x n, where grid[r][c] represents the number of points at position (r, c) on the matrix. Two robots are playing a game on this matrix.

Both robots initially start at (0, 0) and want to reach (1, n-1). Each robot may only move to the right ((r, c) to (r, c + 1)) or down ((r, c) to (r + 1, c)).

At the start of the game, the first robot moves from (0, 0) to (1, n-1), collecting all the points from the cells on its path. For all cells (r, c) traversed on the path, grid[r][c] is set to 0. Then, the second robot moves from (0, 0) to (1, n-1), collecting the points on its path. Note that their paths may intersect with one another.

The first robot wants to minimize the number of points collected by the second robot. In contrast, the second robot wants to maximize the number of points it collects. If both robots play optimally, return the number of points collected by the second robot.

Example 1

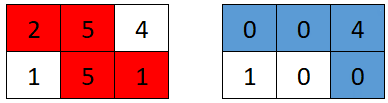
Input: grid = [[2,5,4],[1,5,1]]
Output: 4
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.

Example 2

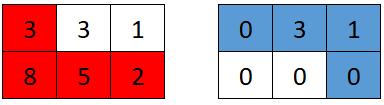
Input: grid = [[3,3,1],[8,5,2]]
Output: 4
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.

Example 3

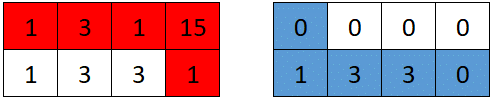
Input: grid = [[1,3,1,15],[1,3,3,1]]
Output: 7
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.

Constraints:

• grid.length == 2
• n == grid[r].length
• 1 <= n <= 5 * 104
• 1 <= grid[r][c] <= 105

Hint 1

There are n choices for when the first robot moves to the second row.

Hint 2

Can we use prefix sums to help solve this problem?

Idea

The first hint is helpful. We could use dynamic programming to solve this question.

We could maintain three states.

1. Sum of untouched grids in the first row, first. Init this as the sum of the first row, because at the start, nothing is touched.
2. Sum of the untouched grids in the second row, second. Init this as 0, because robot 1 could turn down at column 0 and touch all the grids in the second row.
3. The result, res. Robot2 can optimize by either collecting all untouched grids in the first row or the second row. See image below for the two choices. We could init this with a maximum possible number with the given constraints. For each iteration, we update res to be the minimum of 1) res itself and 2) the maximum of the untouched grids in the two rows.

For example, assume robot 1 will turn down at column 1. Robot 2 will then choose to collect all the remaining grids in the first row except grid[0][0]. Therefore, we update second after taking the minimum in step 3 above.

Complexity: Time $O(n)$, Space $O(1)$.

Python

class Solution:
    """85 ms, 29.8 mb"""

    def gridGame(self, grid: list[list[int]]) -> int:
        first, second, res = sum(grid[0]), 0, float('inf')
        for i in range(len(grid[0])):
            first -= grid[0][i]
            res = min(res, max(first, second))
            second += grid[1][i]
        return res

Rust

use std::cmp::{max, min};

/// leet 2017, 0 ms, 3.40 mb

impl Solution {
    pub fn grid_game(grid: Vec<Vec<i32>>) -> i64 {
        let mut first: i64 = grid[0].iter().map(|&x| x as i64).sum();
        let (mut second, mut res) = (0, i64::MAX);
        for i in 0..grid[0].len() {
            first -= grid[0][i] as i64;
            res = min(res, max(first, second));
            second += grid[1][i - 1] as i64;
        }
        res
    }
}