LeetCode 542 LintCode 974 01 Matrix and LeetCode 1765 Map of Highest Peak

Open Table of contents

Description (01 Matrix)
Description (Map of Highest Peak)
Idea1
- Python
- Java
- C++
- Rust
Idea2
- Python

Description (01 Matrix)

Link to Question: LeetCode 542, LintCode 974

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two cells sharing a common edge is 1.

Example 1

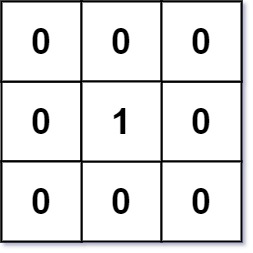
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2

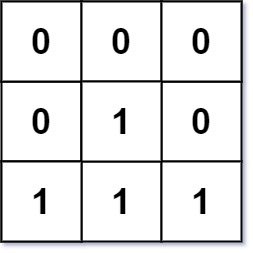
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 10^4
1 <= m * n <= 10^4
mat[i][j] is either 0 or 1.
There is at least one 0 in mat.

Note: This question is the same as 1765: https://leetcode.com/problems/map-of-highest-peak/description/

Description (Map of Highest Peak)

Link to Question: LeetCode 1765

You are given an integer matrix isWater of size m x n that represents a map of land and water cells.

If isWater[i][j] == 0, cell (i, j) is a land cell.
If isWater[i][j] == 1, cell (i, j) is a water cell.

You must assign each cell a height in a way that follows these rules:

The height of each cell must be non-negative.
If the cell is a water cell, its height must be 0.
Any two adjacent cells must have an absolute height difference of at most 1. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).

Find an assignment of heights such that the maximum height in the matrix is maximized.

Return an integer matrix height of size m x n where height[i][j] is cell (i, j)’s height. If there are multiple solutions, return any of them.

Example 1

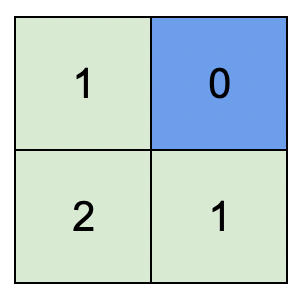
Input: isWater = [[0,1],[0,0]]
Output: [[1,0],[2,1]]
Explanation: The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.

Example 2

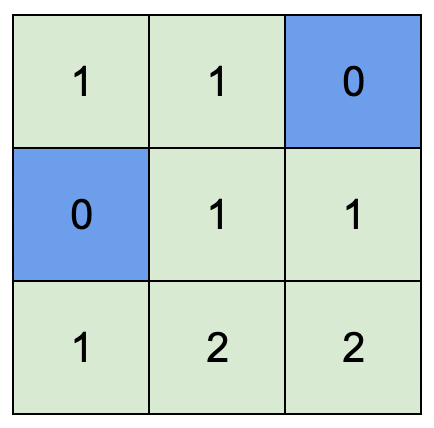
Input: isWater = [[0,0,1],[1,0,0],[0,0,0]]
Output: [[1,1,0],[0,1,1],[1,2,2]]
Explanation: A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.

Constraints:

m == isWater.length
n == isWater[i].length
1 <= m, n <= 1000
isWater[i][j] is 0 or 1.
There is at least one water cell.

Note: This question is the same as 542: https://leetcode.com/problems/01-matrix/

Hint 1

Set each water cell to be 0. The height of each cell is limited by its closest water cell.

Hint 2

Perform a multi-source BFS with all the water cells as sources.

Idea1

The two questions are essentially the same. We could use one line of code to set the value from 1 to 0 and 0 to 1 for the graph.

We could use dynamic programming to solve the question.

We could process the cells from top-left to bottom-right. This way all the cells on the top and left of the current cell have been processed already. We set the cell value to 1 plus the minimum of the two (top, left).

We could then process from bottom-right to top-left. This time we look at cells on the bottom and right of the current cell.

Complexity: Time $O(n)$ , Space $O(1)$ .

Python

class Solution1:
    """
    542, 52 ms, 19.65 mb
    1765, 501 ms, 76.47 mb
    """

    def updateMatrix(self, mat: list[list[int]]) -> list[list[int]]:
        m, n = len(mat), len(mat[0])
        INF = m + n
        for r in range(m):
            for c in range(n):
                # mat[r][c] = 1 - mat[r][c]  # uncomment this line for 1765
                if mat[r][c] > 0:
                    top = mat[r - 1][c] if r > 0 else INF
                    left = mat[r][c - 1] if c > 0 else INF
                    mat[r][c] = min(top, left) + 1
        for r in range(m - 1, -1, -1):
            for c in range(n - 1, -1, -1):
                if mat[r][c] > 0:
                    bottom = mat[r + 1][c] if r < m - 1 else INF
                    right = mat[r][c + 1] if c < n - 1 else INF
                    mat[r][c] = min(mat[r][c], bottom + 1, right + 1)
        return mat

Java

// DP, O(m*n) time, O(1) space (in-place).
class Solution {
    public int[][] updateMatrix(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int INF = m + n;
        for (int r = 0; r < m; r++) {
            for (int c = 0; c < n; c++) {
                if (mat[r][c] > 0) {
                    int top = r > 0 ? mat[r - 1][c] : INF;
                    int left = c > 0 ? mat[r][c - 1] : INF;
                    mat[r][c] = Math.min(top, left) + 1;
                }
            }
        }
        for (int r = m - 1; r >= 0; r--) {
            for (int c = n - 1; c >= 0; c--) {
                if (mat[r][c] > 0) {
                    int bottom = r < m - 1 ? mat[r + 1][c] : INF;
                    int right = c < n - 1 ? mat[r][c + 1] : INF;
                    mat[r][c] = Math.min(mat[r][c], Math.min(bottom + 1, right + 1));
                }
            }
        }
        return mat;
    }
}

C++

// leet 542, DP. O(m*n) time, O(1) space (in-place).
class Solution542 {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>> &mat) {
        int m = mat.size(), n = mat[0].size();
        int INF = m + n;
        for (int r = 0; r < m; r++) {
            for (int c = 0; c < n; c++) {
                if (mat[r][c] > 0) {
                    int top = r > 0 ? mat[r - 1][c] : INF;
                    int left = c > 0 ? mat[r][c - 1] : INF;
                    mat[r][c] = min(top, left) + 1;
                }
            }
        }
        for (int r = m - 1; r >= 0; r--) {
            for (int c = n - 1; c >= 0; c--) {
                if (mat[r][c] > 0) {
                    int bottom = r < m - 1 ? mat[r + 1][c] : INF;
                    int right = c < n - 1 ? mat[r][c + 1] : INF;
                    mat[r][c] = min(mat[r][c], min(bottom + 1, right + 1));
                }
            }
        }
        return mat;
    }
};

Rust

impl Solution {
    pub fn update_matrix(mut mat: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let m = mat.len();
        let n = mat[0].len();
        let inf = (m + n) as i32;
        for r in 0..m {
            for c in 0..n {
                if mat[r][c] > 0 {
                    let top = if r > 0 { mat[r - 1][c] } else { inf };
                    let left = if c > 0 { mat[r][c - 1] } else { inf };
                    mat[r][c] = top.min(left) + 1;
                }
            }
        }
        for r in (0..m).rev() {
            for c in (0..n).rev() {
                if mat[r][c] > 0 {
                    let bottom = if r < m - 1 { mat[r + 1][c] } else { inf };
                    let right = if c < n - 1 { mat[r][c + 1] } else { inf };
                    mat[r][c] = mat[r][c].min(bottom + 1).min(right + 1);
                }
            }
        }
        mat
    }
}

Idea2

We could start from the 0 cells and use breadth-first-search (bfs) to explore the graph. Each step, we process all the cells in the queue, increment the step value and set all the cells explored in this step to that value.

Complexity: Time $O(n)$ , Space $O(n)$ .

Python

class Solution2:
    """
    542, 122 ms, 19.20 mb
    1765, 775 ms, 76.98 mb
    """

    def updateMatrix(self, mat: list[list[int]]) -> list[list[int]]:
        m, n = len(mat), len(mat[0])
        DIR = [0, 1, 0, -1, 0]
        q = deque()
        for r in range(m):
            for c in range(n):
                mat[r][c] = 1 - mat[r][c]  # uncomment this line for 1765
                if mat[r][c] == 0:
                    q.append((r, c))
                else:
                    mat[r][c] = -1  # Marked as not processed
        while q:
            r, c = q.popleft()
            for i in range(4):
                nr, nc = r + DIR[i], c + DIR[i + 1]
                if nr < 0 or nr == m or nc < 0 or nc == n or mat[nr][nc] != -1: continue
                mat[nr][nc] = mat[r][c] + 1
                q.append((nr, nc))
        return mat